Count the number of distinct squares you can draw using only integer co-ordinates for its 4 corners with
the following restrictions.

• The edges should be parallel to the x and y axes

• The x and y co-ordinate of each corner should be within the range 0 to 2*n (range includes 0 and 2*n).

• None of the corners should lie in the central 2*k by 2*k square. It means both x and y co-ordinates of the corners should not lie in the range (n-k) to (n+k) (range inclusive of both ends) at the same time.

Two squares are distinct if and only if at least one of its corners is different.

Note that the edges can go through the central forbidden square. The only condition is that the corners itself should not lie in the central forbidden square.

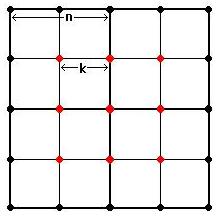
The above figure shows the case n = 2 and k = 1. In the figure the central 2 x 2 square is forbidden and the forbidden lattice points are marked with red. When drawing a square you cannot use these points (marked red) for any of the corners. You are allowed to use only the points marked with black. So the only allowed square you can draw is the 4 x 4 square. Hence the answer for this case is 1.