932 . Divine Rapier +250 dmg
Description
In a fierce combat of dota Kelvin's courier (a creature used to transport player's item) is killed by Godgunman and his +250 damage Divine Rapier dropped on the ground. Because Kelvin's inventory is already full with 6 ironwood branches (and he simply loves them and is unwilling to discard any of them), he decided to quickly hide the divine raiper some place in the bushes, and come back for it later.
However, later on Godgunman destroyed the fortress of Kelvin. Losing his site, Kelvin is forced to go into exile. Until his death he'd never had the chance to return and retrieve his +250 damage Divine Rapier. The hidden place of the Divine Rapier is from then lost, no one knows where it was hidden by Kelvin. However Kelvin had left a treasure map that marked the location he hid his Divine Rapier, now your best friend Dreamoon somehow obtained the map and handed it to you. Gazing at the map (strange, you're completely not interested in finding the Rapier but more obsessed with the beauty of algorithm hidden in the map), you can't help wondering how Kelvin decided where to hide his Rapier.
(If you don't play dota, forget about the story it really isn't important. Below comes the REAL problem.)
Back to years ago... Kelvin is staring at the map, wondering where he could hide his treasure.
The map is a connected graph with EXACTLY n vertices and n edges, furthermore, the degree of each node is between 1 to 4. Now Kelvin wants to hide the Divine Rapier at a particular node which he would then mark as an X. Furthermore in order to avoid the treasure to be discovered accidentally, he also decide that he would NOT hide the Divine Rapier at a node with degree of 4.
Now the question is, given the map, how many different maps are there up to isomorphism (that is, all nodes are considered to have the same looking except for the special X node where the treasure is hidden) after Kelvin marked the big X?
Input Format
Input may contain multiple testcases.
For each testcase, an integer N in the first line specifies the number of vertices. Following is N pair of integers (vi,ui), each representing an undirected edge.
Input ends with EOF.
Output Format
For each testcase output a line: The number of distinct maps up to isomorphism.
N <= 100000
degree of each node <= 4
Sample Input 1
4 1 2 2 3 3 1 1 4
Sample Output 1
3
Hints
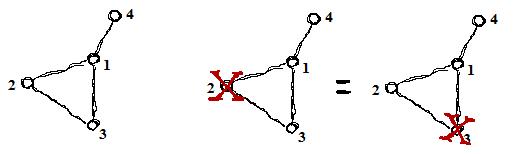
as shown above, the map in the sample input could be marked three ways, since marking X at node 2 and node 3 is equivalent.
Problem Source
Migrated from old NTUJ.
USACO chn07
Subtasks
| No. | Testdata Range | Score |
|---|