933 . Two Parties
Description
King Byteasar has decided to throw two great parties and wants to invite to them every single Byteotian inhabitant. Of course he wants to invite each of them to exactly one of the parties. The king knows from his own vast experience that a person is having a good time when there is an even number of her/his friends at the party. Thus he has asked you to divide the country's inhabitants between two parties in a way that as many people as possible have an even number of friends at their party. A trivial division, i.e. one that leaves one party with no guests invited, is allowed. The acquaintanceship is a symmetric relation, i.e. whenever a person A knows the person B, the person B also knows the person A.
Write a programme that:
* reads from the standard input the number of Byteotia's inhabitants and the description of their acquaintances,<br/>
* splits the inhabitants into two parties in such way that the number of people who have an even number of friends at their party is as large as possible.<br/>
Input Format
For each testcase: In the first line of the standard input there is one integer N (1<=N<=200) - it is the number of inhabitants of Byteotia. The inhabitants are numbered from 1 to N. In the following N lines there are the descriptions of subsequent persons' acquaintances. At the beginning of the (i+1)'th line there is an integer li (0<=li<=N-1) - the number of friends of the ith inhabitant. It is followed by li pairwise distinct numbers of the 'th inhabitant's friends. We assume that no inhabitant is her/his own friend. It follows that each acquaintance is written twice: if A and B know each other, then B appears on A's list of friends and A appears on B's.
There may be multiple testcases. Input ends with EOF.
Output Format
In the first line of the standard output your programme should write one integer - the number of people who are to come to the first party. In the second line the numbers of these people should be written. The rest shall come to the second party.
In case there are many cases that all maximize the number of people with even friends attending same party, let the first guest (guest number 1) come to the first praty if possible; if still mutiple answers exist, let the second guest come to the first party if possible, then the third, and so on.
Sample Input 1
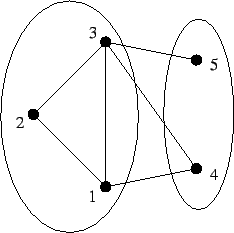
5 3 2 3 4 2 1 3 4 2 1 4 5 2 1 3 1 3
Sample Output 1
3 1 2 3
Hints
The sample test data could be demonstrate as follow:
Problem Source
Migrated from old NTUJ.
poi 12th stage III
Subtasks
| No. | Testdata Range | Score |
|---|