946 . Array Game
Description
There is a single-player game played on a one-dimensional infinite-from-both-ends array containing integers, + signs
and - signs. In each turn, the player can move all integers one cell to the left or one cell to the right (signs remain
fixed).
The player’s initial score is 0; when an integer I moves into a cell containing the sign S (+ or -), the integer is removed from the array and the score is increased by S × I.
The player can stop the game anytime he/she wants.
Below you can see the initial and the following states of the array, after two right moves are made.
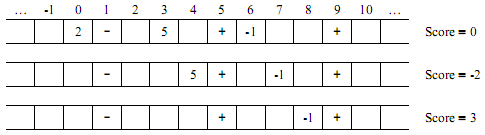
Your task is to find the maximum possible score one can get from a given initial array.
Input Format
There are multiple test cases in the input. The first line of each test case starts with N (1 ≤ N ≤ 1000), the number of
integers, followed by Np (0 ≤ Np ≤ 1000), the number of + signs and Nn (0 ≤ Nn ≤ 1000), the number of - signs. Each
of the next N lines contains two integers pi (−109 ≤ pi ≤ 109), the position and vi (−9 ≤ vi ≤ 9), the value of the i-th integer. The following line contains Np integers indicating the positions of the + signs. The following line contains Nn integers indicating the positions of the - signs. The positions are all between −109 and 109, and no two elements
(integers and signs) are initially placed at the same position. The input terminates with a line containing "0 0 0".
Output Format
For each test case write a single line containing the maximum possible score.
Sample Input 1
3 2 1 0 2 6 -1 3 5 5 9 1 1 1 1 10 5 3 7 0 0 0
Sample Output 1
3 0
Hints
Problem Source
Migrated from old NTUJ.
2009Tehran
Subtasks
| No. | Testdata Range | Score |
|---|