967 . Rectangle of Permutation
Description
We want to build a rectangle where each row is a permutation of 0 to N-1. We want to make this rectangle with as many rows as possible while maintaining the following constraints:
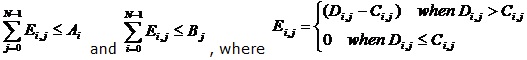
Di,j is the number of occurrences of integer j in the column i. C is a matrix of N rows and N columns will be given as input. A and B are two sequences of size N will be given as input. Given N, A, B, C determine the maximum possible number of rows.
NOTE: the original problem (back in the dhaka regional) actually asked you to FIND a specific rectangle that obey the rules and output it, however here due to special judge issue this task is omitted. But here please, if you would, pretend such requirement exist and think about it a bit before you submit :p
Input Format
First line of the input contains T (1≤T≤50) the number of test cases. Then T test cases follows. Each test case starts with an integer N (1≤N≤30) indicates the number of columns in the rectangle. Next Line contains N integers seperated by a single space. These integers are A0 to AN-1 (0≤Ai≤10). Next line contains N integers separated by a single space. These integers are B0 to BN-1 (0≤Bi≤10). Each of the next N line contains N integers in each lines. The integer on row i and column j is Ci,j (0≤Ci,j≤4) ( i and j starts from zero). A blank line will follow each test case.
Output Format
For each test case output a line in the following format “Case #C: R”. Quotes are for clarity only. C is the test case number starting from 1. R is the maximum possible rows of the rectangle.
Sample Input 1
2 3 0 0 0 0 0 0 2 0 0 0 2 0 0 0 2 3 1 2 3 3 2 1 1 2 3 2 3 1 3 1 2
Sample Output 1
Case 1: 2 Case 2: 7
Hints
for sample testcase 2, we see the following rectangle is valid:
0 1 2
1 0 2
1 0 2
2 1 0
2 1 0
2 1 0
0 2 1
Problem Source
Migrated from old NTUJ.
icpc regional 2009, dhaka site
Subtasks
| No. | Testdata Range | Score |
|---|