Any positive integer v can be written as p1^a1 * p2^a2 * ... * pn^an where pi is a prime number and ai ≥ 0. For example: 24 = 2^3*31.

Pick any two prime numbers p1 and p2 where p1 != p2.
Imagine a two dimensional plane where the powers of p1
are plotted on the x-axis and the powers of p2 on the y-
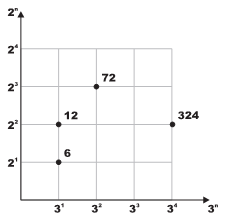
axis. Now any number that can be written as p1^a1 * p2^a2 can be plotted on this plane at location (x, y) = (a1, a2). The figure on the right shows few examples where p1 = 3 and p2 = 2.

This idea can be extended for any N-Dimensional space
where each of the N axes is assigned a unique prime num-
ber. Each N-Dimensional space has a unique set of primes.
We call such set the Space Identification Set or S for short. |S| (the ordinal of S) is N.

Any number that can be expressed as a multiplication of pi ∈ S (each raised to a power (ai ≥ 0)
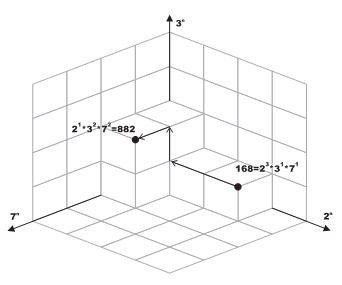
can be plotted in this |S|-Dimensional space. The figure at the bottom illustrates this idea for N = 3 and S = {2, 3, 7}. Needless to say, any number that can be plotted on space A can also be plotted on space B as long as SA ⊂ SB.

We define the distance between any two points in a given N-Dimensional space to be the sum of units traveled to get from one point to the other while following the grid lines (i.e. movement is always parallel to one of the axes.) For example, in the figure below, the distance between 168
and 882 is 4.

Given two positive integers, write a program that determines the minimum ordinal of a space
where both numbers can be plotted in. The program also determines the distance between these
two integers in that space.