987 . Land Division
Description
The king of the Far, Far Away Kingdom has passed-away and the kingdom must be split amongst
his K sons. The kingdom, which can be drawn on a rectangular map, consists of N cities. To
divide the land, they will draw K −1 straight segments on the map, all of them parallel to either
the vertical or the horizontal axis of the map. This divides the map into exactly K rectangles,
all having equal heights (if the dividing lines where vertical), or equal widths (if the dividing
lines where horizontal). No segment should pass through any of the cities. Each son will then
be assigned one random region out of the K regions and the cities inside that region will be his
share.
Of course, they want the division to be as fair as possible: theoretically, in the fairest division,
each son should get N/K cities (we’ll call this value the baseline), but since the baseline isn’t
always a whole number, each of the sons wants to be as close as possible to the baseline. We
will calculate the unfairness of each son as the absolute difference between the number of cities
assigned to him and the baseline. The fairest division is the one that minimizes the average
unfairness of all the sons.
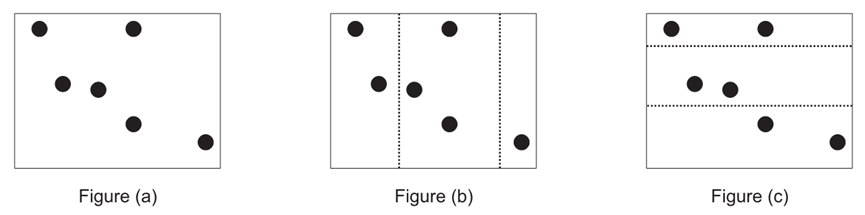
Consider the example above with 3 sons and 6 cities (so the baseline is 6/3 = 2.0) Figure (a) is
the original map. Figure (b) shows a non-optimal division (the dashed lines are the 2 dividing
lines.) In this case, the middle region contains 3 cities (unfairness of |3 − 2| = 1), the left region
contains 1 city (unfairness of |1 − 2| = 1), while the right region contains 2 cities (perfectly fair,
unfairness of 0), so the average unfairness is 2/3.
Figure (c) on the right shows the optimal division since all three regions contain the same number
of cities for an average unfairness of 0.
Write a program to determine the fairest land division for a given kingdom.
Input Format
Your program will be tested on one or more test cases. Each test case is described on N+1 lines.
The first line of each test case specifies two positive integers: (N ≤ 100000) and (K ≤ 10) where
N is the number of cities and K is number of children. Note that K ≤ N.
N lines follows, each describing the coordinates of a city by specifying two integers (x, y) where
0 ≤ x, y ≤ 100000. Since coordinates are rounded to the nearest integer, more than one city
could have the exact same coordinate on the map. You may assume that the map of the kingdom
is any rectangle that contains all of the given points (although such information is not needed by
the program.) Note also that while all cities lie on integer coordinates, the dividing lines need
not be.
The last line of the input file contains two zeros.
Output Format
For each test case, print the following line:
k. A/B
Where k is the test case number (starting at one,) and A/B is the minimum average that could be
obtained. A/B should be an irreducible fraction. Let B=1 when the result is a whole number.
Sample Input 1
6 3 0 4 1 3 2 3 3 1 4 4 5 0 4 3 0 0 0 1 1 1 1 0 0 0
Sample Output 1
1. 0/1 2. 8/9
Hints
Problem Source
Migrated from old NTUJ.
Subtasks
| No. | Testdata Range | Score |
|---|